法国人皮埃尔·德·费马（Pierre de Fermat，1601-1665）是一名律师，与此同时，他也是一位业余数学家。尽管律师才是他的主要职业，但是他在数学方面也取得了完全不亚于其他数学家的成就。费马最喜欢的就是数论。在微积分领域，他的研究也为现代微积分的建立作出了巨大贡献。他是知名数学家贝尔亲口承认的"业余数学家之王"。

陆家羲（1935年6月10日—1983年10月31日），上海人，中国现代数学家，东北师范大学物理系毕业，曾任内蒙古包头市中学教师。1935年生于贫寒家庭，初中辍学后进入哈尔滨电机厂工作。1957年考入吉林师范大学（现东北师范大学）物理系，期间开始研究“寇克满女生问题”。1961年起在包头多所中学任教，业余持续数学研究，1965年完成首篇论文因历史原因未发表。1970年代转向“斯坦纳三元系大集”难题研究。1981年系列论文在国际组合数学界引发关注，被评价为“组合设计理论重大突破”。1983年参加第四届中国数学会年会期间突发心脏病逝世，终年48岁。其成果包括解决“寇克满系列”与“斯坦纳系列”数学难题，论文发表于国际权威期刊。逝世后，1987年获国家自然科学奖一等奖。

猜想：每个大于等于4的偶数都可以表示成两个质数之和。

1742年，哥德巴赫(C.Goldbach，1690一1764)提出了一个假设，每一个大于2的偶数是两个质数的和。但是哥德巴赫自己无法证明它，于是就写信请教赫赫有名的大数学家欧拉帮忙证明，但是一直到去世，欧拉也无法证明。

因现今数学界已经不使用“1也是质数”这个约定，原初猜想的现代陈述为：任一大于5的整数都可写成三个质数之和。（n＞5：当n为偶数，n=2+(n-2)，n-2也是偶数，可以分解为两个质数的和；当n为奇数，n=3+(n-3)，n-3也是偶数，可以分解为两个质数的和）欧拉在回信中也提出另一等价版本，即：任一大于2的偶数都可写成两个质数之和。

常见的猜想陈述为“欧拉版本”，即：任一大于2的偶数都可写成两个质数之和，亦称为“强哥德巴赫猜想”或“关于偶数的哥德巴赫猜想”。

从关于偶数的哥德巴赫猜想，可推出：任一大于7的奇数都可写成三个质数之和的猜想。后者称为“弱哥德巴赫猜想”或“关于奇数的哥德巴赫猜想”。若关于偶数的哥德巴赫猜想是对的，则关于奇数的哥德巴赫猜想也会是对的。

1966年陈景润证明了“1+2”成立。陈景润证明的是1+2，即“任何一个足够大的偶数都可以表示为一个质数加上一个质因数数目不超过2的数”。迄今为止，陈景润1+2是最强结果，虽然离哥德巴赫猜想只有一步之遥，但这一步极其困难。
2013年5月，巴黎高等师范学院研究员哈洛德·贺欧夫各特发表了两篇论文，宣布彻底证明了弱哥德巴赫猜想。

猜想：无论正整数x等于多少，按照规则经过有限次的迭代，最终都可以按4-2-1得到结果1。

考拉兹猜想的迭代过程：始于一个正整数，如是偶数，除以2；如奇数，乘以3再加上1，即3x+1。
考拉兹猜想亦称“冰雹猜想”、“4-2-1猜想”、“3x+1猜想”等。

1930年代，德国汉堡大学的学生考拉兹，曾经研究过这个猜想。
1937年，法国数学家保罗·考拉兹在研究一些数学问题时，提出了一个名为冰雹问题的问题，也就是现在被称为考拉兹猜想。
考拉兹当时的研究对象是所有能被3整除的自然数。他发现，对于任意一个能被3整除的自然数m，不断进行如下变换：将m除以2（如果m是偶数），或者将m乘以3再加1（如果m是奇数），最终一定会得到一个1。 考拉兹的发现并没有得到应有的重视，直到1963年，美国数学家罗伯特·辛格尔（Robert S. Silver）在美国的一场数学大会上提出了这个问题，并将其命名为考拉兹猜想。此后，考拉兹猜想逐渐引起了越来越多数学家的兴趣。 数学家们用计算机已经验证到了\(2^{68}≈2.95 {\times} ^{20}\) ，都满足这个规律，但不意味对所有自然数都是成立的。

陶哲轩 恩师，Paul Erdős: Mathematics is not ready for such problems.
---数学可能还没有为这些问题做好准备。最伟大的数学家们已经放弃了对这个猜想的研究。
---他并称会替找出答案的人奖赏500元。

2025年06月18日 中国学者（知乎网名：大模型掘墓者）首次证明了Collatz conjecture。 本文作者首次发现并揭示了二进制表示下“克拉茨猜想”迭代计算的两个规律：（1）如果在其“最右端”出现“连续1”时，将进行连续的奇数（3n+1）计算，出现“数字快速增长”。（2）将奇数计算(3n+1)改写为(n<<1+n+1)，二进制“进位竖式算式”下自然形成“01错位消融效应”，每一次迭代都能缩短“最右端”的“连续1”，消除了“数字快速增长”的根源，保证迭代过程收敛。通过对剩余情况的补充分析，最终证明了“克拉茨猜想”适用于全部正整数。[本站]

猜想：任意两个相邻完全平方数之间，都存在至少一个质数。即，对任意正整数n，存在质数p，满足 \(n^2\) < p < \((n+1)^2\)。

杰波夫猜想是数论中关于质数分布的重要猜想，1855年由杰波夫（Jie Bove）提出，主张在自然数n的平方 \(n^2\) 与其后继整数 \((n+1)^2\) 之间必定存在质数。
该猜想与孪生质数猜想、布罗卡尔猜想（两质数平方间至少存在4个质数，例如9和25之间存在11、13、17、19、23五个质数）共同构成质数间隔研究的核心命题。现代研究通过质数定理（不可直接用于证明）、邻函数定理等工具构建数论猜想间的逻辑链条，但布罗卡尔命题等关键问题既未被证明也未被推翻。1905年数学家迈伦特率先证明当平方数小于9000000时杰波夫猜想成立。但质数定理不能直接用于杰波夫猜想的证明。

除杰波夫猜想外，还有一个孪生质数猜想，即存在无穷多个p、p+2，p和p+2均为质数。这两个猜想，尤其是杰波夫猜想在国内远不如哥德巴赫猜想有名，但如果说对数学的意义，它们比哥猜要大得多，因为它们关系到质数分布规律之谜。证明和推广这两个猜想，为数论和数学研究打开了一片广阔的天地。
一般人们认为运用质数定理即可证明，但重要的一点“误差”没有考虑到。运用质数定理时一定要注意“x充分大”是指0~x的区间充分大，否则不成立。例如设x是有限数，n充分大，则n~n+x范围内不一定就有质数，因为质数的间隔可以是任意大（这是基本常识，证明可以很容易找到，此略），质数定理也不能直接用于证明杰波夫猜想，因为当 \(x {\rightarrow} \infty\) 时，\({\frac{(x+1)^2}{x^2}} \rightarrow 1\) ，质数定理±5%的误差远远超出了能确认质数存在的要求。

这个猜想最重要的结果是伯特兰-切比雪夫定理：对于任何大于3的自然数n，都至少存在一个质数p满足n<p<2n-2。杰波夫猜想看起来只是伯特兰-切比雪夫定理的一个改进，但这个改进到现在还是没有获得证明。

与杰波夫猜想相关的，还有法国数学家布罗卡尔提出的命题，他认为在两个质数的平方之间至少有 4 个质数，例如在 9 和 25 之间有质数 11、13、17、19、23，但这个命题既没有被证明，也没有被推翻。

猜想：存在无穷多个质数p，使得p + 2是质数。质数对 (p,p+2) 称为孪生质数。

孪生质数就是指相差2的质数对，例如3和5，5和7，11和13…。

在1849年，阿尔方·德·波利尼亚克(Alphonse de Polignac)提出了一般的猜想：对所有自然数k，存在无穷多个质数对(p,p+2k)。k = 1的情况就是孪生质数猜想。

孪生质数猜想正式由希尔伯特在1900年国际数学家大会的报告上第8个问题中提出。
中国数学家张益唐在这个问题上取得了突破性进展，他证明了存在无穷多对质数，它们之间的差距不超过7千万。与2相比较，虽然7千万看起来很大，但以前是完全不能肯定有这样的上限存在，所以张益唐是从无限到7千万的进展，是质的跨越。假如把7千万缩小到2，就证明了孪生质数猜想。目前已经将7千万缩小到了246，但再往下就十分困难了。

梅森质数猜想：存在无穷多个梅森质数。

梅森(Marin Mersenne，1588-1648)是十七世纪的法国数学家，他研究了 \(2^p-1\) 类型的数(p是质数)。后来人们把这样的数叫做梅森数(记为Mp)。如果对于某个p，Mp是个质数则称之为梅森质数。

寻找梅森质数是目前寻找大质数最好的办法。找到更大的梅森质数或者质数，是数论学者的巨大成就。

梅森质数大搜索（GIMPS）是1996年启动的分布式计算项目，通过整合全球志愿者计算机算力搜索梅森质数。项目使用开源软件prime95和MPrime分配计算任务，采用卢卡斯-莱默测试进行质数验证，已累计发现18个梅森质数。截至2024年，覆盖190多个国家近百万参与者，运算峰值超400万亿次/秒。
项目设立3000美元研究发现奖与电子前沿基金会15万美元奖金机制，其研究成果推动数论发展并应用于芯片缺陷检测。近几十年来找到的最大质数都是通过对梅森质数的搜索所得到的。

2016年发现了 \(2^{74207281}-1\) (柯蒂斯·库珀)。
2018年发现了 \(2^{82589933}-1\) 。
2024年发现了 \(2^{136279841}-1\)，具有41024320位十进制数，是首个完全由GPU集群主导完成的发现。

猜想：存在无穷多个自然数n，使得 \(n^2+1\) 是质数。

例如n=1时 \(1^2+1\) =2（质数），n=2时 \(2^2+1\)=5（质数），但n=3时 \(3^2+1\) =10（非质数）。
‌‌ 该猜想尚未被严格证明或否定，属于数论领域开放性问题‌。

‌部分研究尝试通过概率统计法（如质数定理推导）或代数数论（如不可约多项式性质）进行证明，但均未被数学界广泛认可。 ‌ 该猜想与 黎曼猜想 存在间接联系，因后者涉及质数分布规律‌。 该猜想被归类为广义 费马质数 问题，与 孪生质数猜想 、 勒让德猜想 等同属质数分布难题‌。

这个猜想的表述出奇的简单，证明却完全无从着手。数列 \(n^2+1\) 以其表面上的简单性掩盖了深层的复杂性。乍一看，它只是将一个数平方后加 1，但这一简单操作背后隐藏着深刻的数学奥秘。一个长期悬而未决的问题是：这个数列中是否存在无限多个质数？数学家们至今尚未找到明确的答案。然而，研究 \(n^2+1\) 数列的真正意义并不局限于解答这些具体的问题。正如蒙特利尔大学的安德鲁·格兰维尔所指出的，探究这个数列的过程中，人类的知识边界很快就会显现出来。而每一次对这些边界的突破，往往都会催生出新的数学方法。这些方法不仅推动了对加法和乘法之间关系的理解，也在其他数学领域带来了新的洞见。

猜想：费马数中的质数只有有限多。

所谓费马数，是指形如：\(2^{2^n}\) 的数，其中n=0，1，2，3，4……，通常把它记为F(n)。

法国数学家皮埃尔·德·费马(Pierre de Fermat，1601 -1665)发现，当n从0到4时，F(n)的值分别是3、5、17、257和65537，它们都是质数。由于下一个F(5)太大，费马没有去检验，于是他猜测费马数全都是质数。然而将近一百年后，欧拉发现F(5)是个合数，F(5)=641×6700417，推翻了费马的猜想。更令人大跌眼镜的是，后来人们算出的费马数全都是合数，再也没见到一个质数!那么将费马数猜想反过来，是否意味着费马数中只有有限个质数，或再进一步，费马数中的质数是否只有最初的那五个呢？

---

费马大定理(Fermat’s Last Theorem)

费马大定理(Fermat’s Last Theorem)，又被译为“费马最后定理”，在老的文献中也常被称为费马猜想(Fermat’s conjecture)。其断言不存在三个正整数x,y,z使得n大于2时方程\(x^n+y^n=z^n\) (也被称为费马方程)有解。

费马大定理是费马在1637年前后作为一个定理提出的。他在丢番图(Diophantus)的《算术》拉丁文译本的页边空白处陈述了此命题并称自己已经证明，但他的证明在页边的空白处写不下。费马大定理在当时难以证明，因此其常被称为费马猜想而非定理，费马所称的证明也不被承认。无数数学家尝试证明该命题但都以失败告终，直到命题提出358年后的1994年，安德鲁·怀尔斯(AndrewWiles)才成功完成证明，并于1995年正式发表。

奇完全数猜想：是否存在奇完全数？

完全数(perfect number)亦称完满数、完美数，是指它的所有真因数之和等于它自己。注意，真因数不同于是质因数，真因数是指小于它自己的因数，这些真因数中有的可能是合数。例如6是一个完全数，因为6的真因数只有1、2、3，而1+2+3刚好等于6。又如28的所有真因数是1、2、4、7、14，这些数加起来等于28，所以28也是完全数。

截止2018年，已经找到了51个完全数，它们全都是偶数，且都能表示成Mp+1(Mp为梅森质数)。
截至2024年，人类发现的51个完全数对应的指数 p 均为质数(即 \(2^p+1\) )，具体如下：
第1个完全数的指数：p = 2，3，5，7，13，17，19，31，61，89，107，127，521，607，1279，2203， 2281，3217，4253，4423，9689，9941，11213，19937，21701，23209，44497， 86243，110503，132049，216091，756839，859433，1257787，1398269，2976221， 3021377，6972593，13466917，20996011，24036583，25964951，30402457， 32582657，37156667，42643801，43112609，57885161，74207281，77232917，82589933

目前完全不清楚。假如存在奇的完全数，那么它必须要大于 \(10^{1500}\) 。

猜想：是否存在完美长方体？

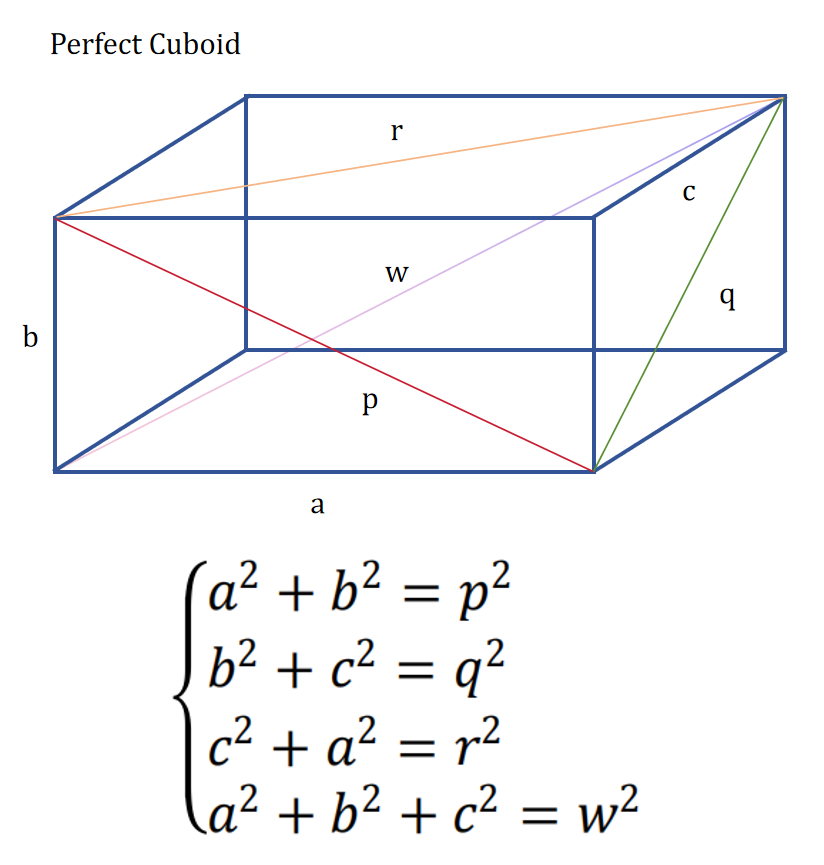
记长方体的长宽高为a、b、c是三个正整数，如果三条“面对角线”的长度： \(\sqrt{a^2+b^2}\)、 \(\sqrt{b^2+c^2}\)、 \(\sqrt{c^2+a^2}\) 和“体对角线”的长度 \(\sqrt{a^2+b^2+c^2}\) 都是正整数，那么这样的长方体就是“完美长方体”。

我们只知道勾股数，但三个平方数相加在什么情况下是平方数还没有解决，所以完美长方体是否存尚不能证明或也不能证伪。数值验证表明，如果存在完美长方体，那么它最小的奇数棱长不小于 \(2.5×10^{13}\)。

2025年06月27日 中国学者（知乎网名：大模型掘墓者）首次证明了完美长方体猜想。 本文作者利用完美平方数的多个特性，完全筛选了所有可能的平方数，均无法满足丢番图方程。证明了玩美长方体是不存在的。首次破解了几百年来的谜团。[本站]

猜想：常数γ是一个有理数还是无理数？

这个常数源于欧拉证明了所有自然数的倒数和 \(1+{\frac{1}{2}}+{\frac{1}{3}+...+{\frac{1}{n}}+...}\) 是发散的，而它发散的速度是Inn。这说明 \(1+{\frac{1}{2}}+{\frac{1}{3}+...+{\frac{1}{n}}-Inn}\) 在n趋于无穷时会趋于一个极限，这个极限现在被称为欧拉-马歇罗尼常数。马歇罗尼(Lorenzo Mascheroni，1750-1800)是一位意大利数学家，他把这个常数记为γ，并把它算到了小数点后32位，但后来人们发现他在第20位出现了错误。尽管如此，马歇罗尼通过对这个常数的研究还是把他的名字刻在了数学史上。

现在我们知道，γ约等于0.57721。

直觉上，它是无理数的概率显然比它是有理数的概率大得多——但目前完全无法证明。
其实数学里还有很多类似的问题，如圆周率π和自然对数的底e都早已证明了是无理数，但π+e是不是无理数目前就没人知道!

猜想：如果A是一个正整数的无穷子集，而且A中所有数的倒数和发散，那么A包含任意长度的等差数列。

该猜想表述为：对于所有n>1的正整数，方程 \[{\frac{4}{n}}={\frac{1}{x}}+{\frac{1}{y}}+{\frac{1}{z}}\] 都有正整数解x、y、z。例如，当n =2时， \[{\frac{4}{2}}={\frac{1}{1}}+{\frac{1}{1}}+{\frac{1}{1}}\] 当n =3时， \[{\frac{4}{3}}={\frac{1}{1}}+{\frac{1}{3}}+{\frac{1}{3}}\] 目前，虽然已经证明除了n同余于1，
\[1，121，169，289，361(mod 840)\] 之外，此猜想皆成立，但它仍然是一个尚未完全解决的问题1。该猜想在数论领域具有重要地位，吸引了众多数学家和数学爱好者进行研究，对于推动数论的发展具有积极作用。
因为所有自然数的倒数和发散，所以会有它的子集也满足倒数和发散。但为什么这会导致A包含任意长度的等差数列，埃尔德什的思路真是天马行空!一个有趣的特例是所有质数的集合，格林和陶哲轩证明了所有质数的倒数和发散，而且所有质数中包含任意长度的等差数列。这个成果帮助陶哲轩得到菲尔兹奖。

猜想：对于任何一个大于1的自然数k是否都存在某个数g(k)，使得任何自然数都可以表示成不超过g(k)个k次方数之和？

英国数学家华林(Edward Waring，1736-1798)发现，每一个自然数都可以表示成最多9个立方数之和，也可以表示成最多19个四次方数之和。于是他问，对于任何一个大于1的自然数k是否都存在某个数g(k)，使得任何自然数都可以表示成不超过g(k)个k次方数之和？

希尔伯特(David Hilbert，1862-1943)给出了肯定的回答：对于任意一个k，都存在相应的g(k)。但他只是证明了g(k)的存在性，如何把g(k)用k表示出来还不清楚。后来数学家们找到了一个g(k)的表达式，唯一的问题是……它其实不是一个表达式，而是三个表达式，分别对应三种可能的情况。然后，数学家猜测这三种情况中只有第一种会发生，那么答案就会简化到只剩第一个表达式。

猜想：如果有两个互质的自然数a和b，它们的和a+b=c，那么在绝大多数情况下，abc的根积rad(abc)>C。

所谓根积(radical)，就是先把一个自然数分解成所有质因数的乘积，然后把所有的质因数相乘一次(无论某个质因数出现了多少次都只乘一次)。例如10=2×5，它的根积就是2×5=10;12=2×2×3，它的根积就是2×3=6。

数论中的abc猜想(亦以Oesterlé–Masser猜想 而闻名)最先由乔瑟夫·奥斯达利（Joseph Oesterlé）及大卫·马瑟（David Masser）在1985年提出。若d是abc不同素因数的乘积，这个猜想本质上是要说d通常不会比c小太多。换句话来说，如果a，b的因数中有某些质数的高幂次，那c通常就不会被质数的高幂次整除。

abc猜想因它所带来的一些关于数论的有趣的结论而著名，很多著名的猜想和定理都紧接着abc猜想问世 。

数学家Goldfeld (1996)认为abc猜想是“the most important unsolved problem in Diophantine analysis”。

Lucien Szpiro（法国数学家，因其在数论、算术代数几何和交换代数上的贡献而知其名）在2007年时尝试攻克此猜想，但后被证明其中有误。

在2012年8月，日本的京都大学数学家望月新一（mochizuki shin'ichi）发布了其四篇预印文稿，介绍了他的Inter-universal Teichmüller theory（宇宙际Teichmüller理论），并声称用此理论可证明包括abc猜想在内的几个著名猜想。他的论文在数学期刊上刊登以供参考查阅，很多人也开始学习他的理论。很多数学家对他的文章持怀疑态度，也正是因为他这篇古怪晦涩的证明，我们知道了，要解决这个猜想或许还是要走上孤独的漫漫长路。不变的是，在我们试证明其正误之时，数学水平得到提高，也终将找到解决abc猜想之路。

ABC猜想还有一个非常讨厌的地方，它说的不是一定如此，而是“在绝大多数情况下”。为什么会这样，以及如何精确地表示“绝大多数情况”，可参看相关介绍文章。如果证明了ABC猜想，就能快速地证明费马大定理。

猜想：方程 \(S_m(n)=(n+1)^n\) 仅有平凡解m=1，n=2(即1+2=3)。

Bowen猜想是数论中的一个经典丢番图方程问题，主要研究连续自然数的幂和是否等于下一个数的幂。
其核心命题为：
方程 \(S_m(n)=(n+1)^n\) 仅有平凡解m=1，n=2(即1+2=3)，
其中 \(S_m(n)=1^m+2^m+.…+n^m\)。

猜想：不等式表述对于任意矩阵 \(A∈F^{s×n}\) 和 \(B∈F^{n×m}\) ,有：rank(AB)≥rank(A)+rank(B)-n。

Sylvester不等式是矩阵理论中的经典结果，描述了两个矩阵乘积的秩与其因子秩之间的关系。其猜想形式和推广在矩阵分析、线性代数等领域具有重要研究价值。以下是其核心内容、推广形式及研究进展的详细分析：
不等式表述对于任意矩阵 \(A∈F^{s×n}\) 和 \(B∈F^{n×m}\) ,有：rank(AB)≥rank(A)+rank(B)-n

证明方法

分块矩阵技巧：通过构造分块矩阵并利用初等行变换，证明n+rank(AB)≥rank(A)+rank(B)。

线性映射视角：将矩阵乘积视为线性变换的复合，结合核与像的维数关系推导不等式。

方程组分析：通过分析矩阵列向量的线性相关性，建立秩的下界。

猜想：对于任意正实数 \(x_1,x_2...,x_n\) ,其混合算术平均值不超过混合几何平均值，且当且仅当所有 \(x_i\)相等时等号成立。

Holland猜想是不等式理论中的一个重要问题，主要涉及混合算术-几何平均值的比较关系。以下是其核心内容、证明进展及推广形式的详细分析：
由数学家F.Holland于1992年提出，其核心命题为：
对于任意正实数 \(x_1,x_2...,x_n\) ,其混合算术平均值不超过混合几何平均值，且当且仅当所有 \(x_i\)相等时等号成立。
具体形式可表示为：
\[\frac{1}{n}\sum_{i=1}^{n}{x_i}≥\prod_{i=1}^{n}{{x_i^{1/n}}}\] 但需注意，此处的“混合平均”并非传统意义上的算术与几何平均，而是通过特定权系数或递归关系构建的广义平均值。

猜想：证明(sophomore's dream)恒等式成立。

1697年的某一天，闲来无事的约翰·伯努利 (Johann Bernoulli) 公布了两条恒等式，并为之命名为二年级之梦 (sophomore's dream)：
\[\int_{0}^{1}{{x^{-x}}}\mathrm{}dx=\sum_{n=1}^{\infty}{{n^{-n}}}\mathrm{ } (=1.2912859970.….)\]
\[\int_{0}^{1}{{x^{x}}}\mathrm{}dx=\sum_{n=1}^{\infty}{{(-n)^{-n}}}\mathrm{ } (=0.7834305107.….)\] “Sophomore's Dream”(大二学生的梦)是一个有趣的数学恒等式。它主要涉及到两个看似不相关的积分结果之间的奇妙联系。具体内容为：
\[\int_{0}^{1}{{x^{-x}}}\mathrm{}dx=\sum_{n=1}^{\infty}{{n^{-n}}} \]
\[\int_{0}^{1}{{x^{x}}}\mathrm{}dx=\sum_{n=1}^{\infty}{{(-1)^{n-1}}n^{-n}} \]
这个结果最早由数学家约翰・伯努利发现，但当时没有给出严格证明。后来，在 19 世纪，通过更深入的数学分析和理论才逐步得到了严格的证明。“Sophomore's Dream” 这个名称暗示着这个结果对于一个大二学生来说，就像是一个意想不到的美妙梦境，因为它展示了积分与无穷级数之间一种非常奇特和美妙的关系，这种关系并不是一眼就能看出来的，需要运用到一些较为高深的数学知识和技巧才能理解和证明。

猜想：除了 \(8=2^3\) ，\(9=3^2\) 以外，没有两个连续数都是正整数乘幂。

凯特兰猜想是数论中的一个著名猜想，由比利时数学家欧仁·查理·卡塔兰(Eugène Charles Catalan)于1844年提出。

即不定方程 \(x^p-y^q=1\) ，其中p，q均是质数，x，y，p，q为正整数，除了(x，y，p，q)=(3，2，2，3)这一组解外，没有其他的正整数解。

在卡塔兰之前，1320年左右，莱维·本·热尔松就证明了2和3的幂之间只有8和9相差是1。
卡塔兰猜想提出后，数学家们进行了大量研究。
1850年，维克多-阿梅代·勒贝格解决了b=2的情况。
1976年，罗伯特·泰德曼证明卡塔兰猜想的方程只有有限个解。
1999年，莫里斯·米尼奥特证明如果存在非平凡解，那么 \(a，b\lt10^{10^{10^{10}}}\)。
2002年4月，帕德博恩大学的罗马尼亚数学家普雷达·米哈伊列斯库证明了这一猜想，使其成为定理。 这个证明由尤里·比卢检查，大幅使用了分圆域和伽罗华模。

相关推广：1986年，肖里和泰德曼将凯特兰猜想扩展到了有理数的范围，提出广义凯特兰猜想。此外，皮莱猜想把凯特兰猜想一般化，推测正整数的幂之间的差趋向无限大，即对任何正整数，仅有限多对正整数的幂的差是这个数，该猜想仍未解决。

猜想：对于任意一个正数 \(k\not\equiv\pm4(mod9)\) ，丢番图方程 \(k=x^3+y^3+z^3\) 有无穷多组整数解(z，y，z)。

1992年，牛津大学Roger Heath-Brown在研究弱近似原则失效形式
\[x^3+y^3+z^3=kw^3\] 的零点密度问题时，提出了一个猜想：
对于任意一个正数 \(k\not\equiv\pm4(mod9)\) ，丢番图方程 \(k=x^3+y^3+z^3\) 有无穷多组整数解(z，y，z)。
(如果没学过初等数论的话，就把 \(k\not\equiv\pm4(mod9)\) 看作 k≠9n±4，也就是 k≠9n+4 或 k≠9n+5。)
如今这个猜想没有得到证明，而且，人们求解丢番图方程\(k=x^3+y^3+z^3\) 的过程也是困难重重。

到2015年，100以内未解决的整数就剩下33、42和74。

2016 年，Sander G. Huisman：
\[74 =(-284650292555885)^3+66229832190556^3+283450105697727^3\]
2019 年，布里斯托大学的Andrew Booker：
\[33 = 8866128975287528^3+(-8778405442862239)^3+(-2736111468807040)^3\]
2019 年 9 月，Andrew Booker 与 大神Andrew Sutherland组队：
\[42 =(-80538738812075974)^3+80435758145817515^3+12602123297335631^3\] \[906=(-74924259395610397)^3+72054089679353378^3+35961979615356503^3\]
虽然100以内的整数立方和的整数解已全部找到，但问题还没有得到解决。
点击查看1-100全部整数解...
1000以内还有很多没找到解的整数：114,165,390,579,627,633,732,906,921 和 975。
数学家们至今也没能证明这个猜想是对的。
面对越来越多的未解整数，这个坑显然不是一个简单的坑。

猜想：设k≥1，则方程 \(x^p-y^q=k\) 只有有限个满足x，y，p，q≥2的正整数解。

不难看出，当k=1时，Pillai猜想就变成了Catalan猜想.
\[a^x-b^y=c \mathrm{} \quad (1.1)\] 1936年，赫施菲尔德[He]证明了当(a,b)=(3,2)且|c|足够大时，方程(1.1)在正整数x和y中至多有一个解。
同年，皮莱将这一结果推广到一般(a,b)满足gcd(a，b)=1且a>b≥2的情况，前提是|c|>co(a，b)。
由于皮莱的工作(以及赫施菲尔德的研究)依赖于西格尔对图氏定理的改进——该定理涉及有理逼近代数数的方法——因此这些结论并不具有有效性(因为从证明过程中无法计算出co(a，b))。
1945年，S.S. Pillai 在论文中提出猜想。
这一猜想一直悬而未决，直到1982年斯特罗克和蒂杰曼通过建立代数数对数线性形式的下界证明了该猜想，其方法类似于贝克的早期无证明主张。随后，斯科特[Sc]利用二次域中整数的性质给出了初等证明。

猜想：方程 \(x^p+y^q=z^r\) 没有满足条件(x，y，z)=1，p，q，r>2的正整数解.

比尔猜想是数论领域的一个未解难题，由美国银行家D·安德鲁·比尔（Andrew Beal）于1993年提出。Beal猜想到目前为止也尚未得到证实，但若ABC猜想，则可推出Beal猜想也成立.Beal对他的猜想做出了巨额悬赏：他将会奖给第一个解决或否定Beal猜想的人100万美金!

猜想：寻找满足方程 \(n!+1=m^2\) 的整数n和m的值。

Brocard问题是一个数论领域的数学问题，由法国数学家亨利·布罗卡德(Henri Brocard)在1876年和1885年的两篇文章中提出。1913年斯里尼瓦萨·拉马努金(Srinivasa Ramanujan)又独立提出。

满足该方程的数对(n，m)被称为布朗数。截至2023年2月，已知的布朗数只有三对：(4，5)、(5，11)和(7，71)，即4!+1=5²=25，5!+1=11²=121，7!+1=71²=5041。

保罗·埃尔德什(Paul Erdós)猜想不存在其他解。
1993年，Overholt表明如果abc猜想正确，那么该方程只有有限多个解。
2000年，Berndt和Galway对n进行了高达 \(10^9\) 的计算，未发现其他解。
2017年，Matson将计算范围扩大到一万亿，也没有找到更多的解。

猜想：方程 \(1^n+2^n+3^n+…+m^n=(m+1)^n\) 只有正数解n=1，m=2，即1+2=3。

波文猜想是一个关于等幂和问题的数学猜想。

该猜想由瑞士数学家雅各布·伯努利在研究等幂和问题时引出，后被正式提出。截至2012年，对于n=1，2，…，325，该猜想已被验证成立，但尚未得到一般性的证明。

猜想：从196出发，究竟能否加出回文数来？196究竟特殊在哪儿？

如果一个数正读反读都一样，我们就把它叫做“回文数”。随便选一个数，不断加上把它反过来写之后得到的数，直到得出一个回文数为止。例如，所选的数是67，两步就可以得到一个回文数484：
67 + 76 = 143
143 + 341 = 484
把69变成一个回文数则需要四步：
69 + 96 = 165
165 + 561 = 726
726 + 627 = 1353
1353 + 3531 = 4884
89的“回文数之路”则特别长，要到第24步才会得到第一个回文数，8 813 200 023 188。
大家或许会想，不断地“一正一反相加”，最后总能得到一个回文数，这当然不足为奇了。事实似乎也确实是这样的——对于几乎所有的数，按照规则不断加下去，迟早会出现回文数。不过，196却是一个相当引人注目的例外。数学家们已经用计算机算到了3亿多位数，都没有产生过一次回文数。从196出发，究竟能否加出回文数来？196究竟特殊在哪儿？这至今仍是个谜。

猜想：杨辉三角中，出现次数最多的数字自然是1，有无穷多个。那么除了1之外，哪个数字出现的最多呢？

1971年，数学家戴维-辛马斯特通过某种不知道...的方法提出，某个正整数在杨辉三角中出现的次数，存在一个上限，这个上限是多少还不知道，有可能是8，也有可能是10或12。那么到底存不存在这个上限，这个上限又是多少？数学界还没有答案。
图2所示为杨辉三角,其中数字1出现了无穷多次。除了数字1以外，哪个数字出现的次数最多呢?6出现了3次，不过不算多。10出现了4次，不过也不算多。120出现了6次，算多了吧?还不算多。目前已知的出现次数最多的数是3003,它同时等于 \(C_{3003}^{1}\)、\(C_{3003}^{3002}\)、\(C_{78}^{2}\)、\(C_{78}^{76}\)、\(C_{15}^{5}\)、\(C_{15}^{10}\)、\(C_{14}^{6}\)、\(C_{14}^{8}\),在杨辉三角中出现了8次。有没有出现次数更多的数，目前仍然是一个未解之谜。
杨辉三角又叫做帕斯卡(Pascal)三角，是一个由正整数构成的三角形数阵，其生成规律非常简单：每行左右两头的数都是1,中间的数都是它左上角的数和右上角的数之和。在代数和组合数学中，杨辉三角都有着非常重要的意义。如果把首行称做第0行”(因而第二行就叫做“第1行”),把每行的头一个数叫做第0个数”(因而第二个数才是“第1个数”)的话，那么杨辉三角第m行的第”个数就等于\({(1+x)}^m\)的展开式中的m次项系数，也是从m个不同物体中取出其中n个物体的方案数\(C_{m}^{n}\)。在后文中，我们还会提到杨辉三角。
真正精彩的来了。如果把正整数a>1在杨辉三角中出现的次数记做N(a),那么函数N(a)是以什么级别上涨的呢？1971年，戴维·辛马斯特(David Singmaster)证明了N(a)=O(loga),即N(a)最多是以对数级别上涨的。他同时猜想N(a)=0(1),即N(a)有一个上限。这也就是辛马斯特猜想。由于我们一直没能找到出现次数超过8的数，因而这个上界很可能就是8。不过，辛马斯特猜测这个上界更可能是10或者12。
保罗·埃尔德什(Paul Erdos)认为，辛马斯特的猜想很可能是正确的，但证明起来会非常困难。

猜想：丢番图方程 \((xn)^x+(bn)^y=(cn)^z\) 除了x = y = z = 2外，没有其他正整数解。

Jeśmanowicz 猜想是关于商高数（也称为毕氏三元数）的一个数论猜想。对于满足 \[a^2+b^2=c^2\] 的正整数三元组(a, b, c)（即商高数），Jeśmanowicz 猜想指出，丢番图方程 \[(xn)^x+(bn)^y=(cn)^z\] 除了x = y = z = 2外，没有其他正整数解。

例如，当(a, b, c)=(3, 4, 5)时，就是常见的勾股数组合，Jeśmanowicz 猜想认为对于任意正整数n，方程 \[(3n)^x+(4n)^y=(5n)^z\] 只有x = y = z = 2这一组正整数解。

这个猜想自提出以来，虽然已经有许多数学家对其进行了大量研究，并在一些特殊情况下证明了该猜想成立，但目前还没有得到完全的证明。例如，1993 年，K. Takakuwa 和 Y. Asaeda 证明了如果m是奇数，p是个奇质数且 \(p{\equiv}3(mod 4)\) ，当 \(y{\ne}1\) 时，则不定方程 \((4m^2-p^2)^x+(4mp)^y=(4m^2+p^2)^z\) 的正整数解只有(x, y, z)=(2, 2, 2)。

四立方和问题是数论中的一个研究课题，主要探讨的是关于将整数表示为四个整数的立方和的相关问题。

与四平方和定理（每个正整数均可表为四个整数的平方和）类似，人们自然会思考对于立方和的情况是否有类似的结论。然而，立方和的情况要复杂得多。

对于四立方和问题，目前并没有像四平方和定理那样简洁明确的一般性结论。虽然对于一些特定的整数，能够找到其表示为四个整数立方和的方式，但要确定任意整数是否都能表示为四个整数的立方和，以及如果能表示，如何找到这样的表示，都是尚未完全解决的问题。

例如，对于某些较小的整数，可以通过尝试和计算找到其立方和表示。像1729这个数，它可以用两种不同方式写成两个正整数的完全立方的和，即\(1729=1^3+12^3=9^3+10^3\),但这与四立方和问题的一般情况有所不同。

在研究四立方和问题的过程中，数学家们也在不断探索各种方法和思路，试图找到更一般性的规律和结论。例如，通过分析整数的一些性质、利用数论中的一些工具和定理来进行研究，但至今仍未取得像四平方和定理那样完善的成果。

猜想：方程 \(x^p+y^q=z^r\) 满足条件 (x,y,z)=1, \({\frac{1}{p}}+{\frac{1}{q}}+{\frac{1}{r}}<1\) 的正整数解只有有限个。

不难看出，当p=q=r>3时，Fermat-Catalan猜想就变成了Fermat大定理。而当x=1时，Fermat-Catalan猜想就变成了Catalan猜想。

若Fermat-Catalan猜想不成立，则有无穷多个abc-三元数组 \(x^p+y^q=z^r\) 满足 \[rad(x^p·y^q·z^r)^{1+{\frac{1}{41}}}=rad(xyz)^{\frac{42}{41}}≤(xyz)^{\frac{42}{41}}<(z^{\frac{r}{p}}·z^{\frac{r}{q}}·z)^{\frac{42}{41}}=z^{r({\frac{1}{p}}+{\frac{1}{q}}+{\frac{1}{r}})·{\frac{42}{41}}}≤z^{r·{\frac{42}{42}}·{\frac{42}{41}}}=z^r\] 这与abc猜想的结论矛盾，从而Fermat-Catalan猜想成立。

遗憾的是，Fermat-Catalan猜想尚未被证明。

猜想：吉尔布雷思对于所有质数都成立吗？

从小到大依次列出所有的质数：2， 3， 5， 7， 11， 13， 17， 19， 23， 29， 31， …
求出相邻两项之差：1， 2， 2， 4， 2， 4， 2， 4， 6， 2， …
现在，再次求出所得序列中相邻两项之差，又会得到一个新的序列：
1， 0， 2， 2， 2， 2， 2， 2， 4， …
重复对所得序列进行这样的操作，我们还可以依次得到
1， 2， 0， 0， 0， 0， 0， 2， …
1， 2， 0， 0， 0， 0， 2， …
1， 2， 0， 0， 0， 2， …
1， 2， 0， 0， 2， …
大家会发现一个有趣的规律：每行序列的第一个数都是1。
某日，数学家诺曼•吉尔布雷思（Norman L. Gilbreath）闲得无聊，在餐巾上不断对质数序列求差，于是发现了上面这个规律。吉尔布雷思的两个学生对前64 419行序列进行了检验，发现这个规律始终成立。1958年，吉尔布雷思在一个数学交流会上提出了他的发现，吉尔布雷思猜想由此诞生。
这个规律如此之强，很少有人认为猜想不成立。1993年，安德鲁•奥德里兹科（Andrew Odlyzko）对10 000 000 000 000以内的质数（也就是346 065 536 839行）进行了检验，也没有发现反例。
不过，这一看似简单的问题，几十年来硬是没人解决。

猜想：质数最大间隙满足 \(G(X)=sup_{pn}≤X(P_{n+1}-P_n)=(logX)^{2+o(1)}\).

克拉梅尔猜想是瑞典数学家哈拉尔德·克拉梅尔(Harald Cramér)在1937年提出。
基于随机模型预测质数间隙的极端行为，反映质数分布的“不规则性”。
根据质数定理，质数平均间距约为log X,因此早期研究关注G(X)与log X的关系。注意，这里的 \(log_{n}{X}=log {\circ} log {\circ} … {\circ} log(X)\) 的意思。

猜想：当 \(n≥1\) 时， \(p_n\) 均为质数。
由大数学家集合论的创始人 Georg Ferdinand Ludwig Philipp Cantor 提出该猜想。其中：
设 \(p_1=2\)，当 \(n≥2\) 时，\(p_n=2^{p_{n-1}}-1\) 。
\(p_1=2\)
\(p_2=2^2−1=3\)
\(p_3=2^3−1=7\)
\(p_4=2^7−1=127\)
\(p_5=2^{127}-1=170141183460469231731687303715884105727\)
\(p_6=2^{170141183460469231731687303715884105727}-1\)

Cantor 猜想不仅证明无望，甚至连验证都无比地困难。
比如：显然 \(p_1\)，\(p_2\)，\(p_3\)，\(p_4\) 都是质数，但要判断\(p_5\) 是质数却很难。
而\(p_6\) 设置连计算都十分困难，因为这个数的位数为： \[\left[ \log_{10}(2^{170141183460469231731687303715884105727}-1) \right]+1\] \[=\left[ 170141183460469231731687303715884105727\log_{10}2 \right]+1\] \[=51217599719369681875006054625051616350\]
而目前已知的最大质数： \[M_{136279841}=2^{136279841} − 1\] 也才不过 41024320 位。所以对于 Cantor 猜想不要说证明，仅仅是验证 n=6 的情形都十分困难。由此可见 Cantor 猜想是一个令人感到绝望的猜想。
但是若某一天有人证明了\(p_6\) 是一个合数，则不仅能够一举否定 Cantor 猜想，还能知道当 n≥6 时， \(p_n\) 均为合数，也就是说 Cantor 猜想OVER。

猜想：若线性函数组 \(L_i(n)=a_{i}n+b_{i}\) ，对任意质数p，存在 \(n_p\) 使得 \(\prod_{i=1}^k{L_i}\left({n_p}\right)\) 与p互素，则存在无限多n使所有 \(L_i(n)\) 为质数。

k生素数是数学中描述素数间隔规律的术语，指由k个依次相差给定正偶数的素数组成的集合，其中k>1。例如当k=2时，间隔为2的称为孪生素数，间隔更大的则为广义孪生素数。
其核心特征在于：对于给定递增正偶数序列d₂ < …ₖ，若存在素数p₁使得p₁, p₁+d₂,…,p₁+dₖ均为素数，则构成k生素数。当这些间隔形成等差数列时，即成为素数等差数列。研究证明无限长的素数等差数列不存在，且当首项素数大于k时，公差必须被所有不大于k的素数整除。
相关研究始于1923年哈代与李特尔伍德提出的广义k生素数猜想，并给出渐近公式。1927年爱尔特希–图兰猜想认为素数中存在任意长度等差数列，该猜想在2004年被格林与陶哲轩证明成立，但具体构造依然困难。当k=1时，理论对应素数定理及其在等差数列中的推广形式已被证实。

质数分布是数论中研究质数性质的重要课题。质数或称质数，是指一个大于1的整数，除1和它本身外，不能被其他的正整数所整除。研究各种各样的质数分布状况，一直是数论中最重要和最有吸引力的中心问题之一。

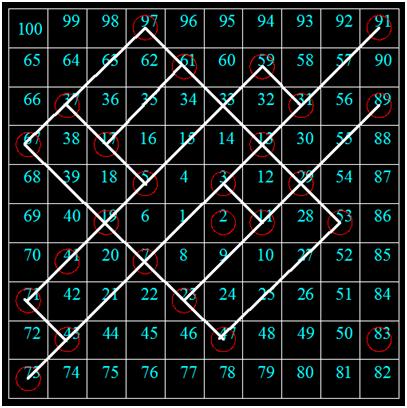
大约在公元前300年，欧几里得就证明了质数有无穷多个。设2,3,…,p是不大于p的所有质数，q=2*3*…*p+1。容易看出q不是2，3，…，p的倍数。由于q的最小正除数一定是质数，因此，或者q本身是一个质数，或者q可被p与q之间的某两个质数所整除[比如：2*3*5*7*11*13+1=30031=59*509]。所以必有大于p的质数存在，由此即知质数有无穷多个。
质数在自然数中占有极其重要的地位，但是它的变化非常不规则。最初的研究方法，是通过观察质数表来发现质数分布的性质。现有的较完善的质数表是D.B.扎盖尔于1977年编制的，列出了不大于50000000的所有质数。从质数表可以看出：在1到100中间有25个质数，在1到1000中间有168个质数，在1000到2000中间有135个质数，在2000到3000中间有127个质数，在3000到4000中间有120个质数，在4000到5000中间有119个质数，在5000到10000中间有560个质数。

1963年，美籍波兰物理学家乌拉姆在参加一个学术会议时比较无聊，就信手把自然数按照逆时针方向排成螺旋状以消磨时间。没想到，乌拉姆意外的发现画出来的数字螺旋中，质数都排列在一条条直线上。后来，他和同事们一起用计算机计算了1000万以内的自然数，发现质数仍然在直线上。
当然，这不能叫做一个数学规律，只能叫做某种蛛丝马迹，成因尚不清楚。其实，类似的现象还有萨克斯螺旋。后来不断有数学家试图给出必然得到质数的公式，也确实有一些这样的公式。

质数定理

关于质数个数的研究是质数分布中最重要的问题之一。以 π(x)表示不大于x的质数个数，例如，π(2)=1，π(3)=2，π(100)=25，π(1000)=168。欧几里得早就证明了质数有无穷多个，即。从表可以看出：①x越大,π(x)与x的比值越接近于0；②x越大,π(x)与x/lnx的比值越接近于1。A.-M.勒让德和C.F.高斯猜测即通常所称的质数定理。它是质数分布理论的中心定理。在这方面首先做出贡献的是∏.Л.切比雪夫，他在1852年左右证明了存在两个正常数с1,с2，使得不等式с1x/lnx≤π(x)≤с2x/lnx成立，其中x≥2。在1896年，J.（-S.）阿达马和C.瓦莱·普桑彼此独立而又几乎同时证明了质数定理。他们的证明都使用了高深的复变函数论知识。因此，能否以尽可能初等的方法来证明质数定理，则成为数学家一直探讨的重要问题。1949年，A.赛尔伯格和P.爱尔特希给出了质数定理的初等证明，除了极限、lnx和e的性质之外，没有用到其他的分析知识，但证明过程十分复杂。他们的证明是基于赛尔伯格的著名恒等式。
有误差项的质数定理是指寻求误差π(x)-lix的最佳估计,,它比x/lnx更接近于π(x)。C.瓦莱·普桑于1900年首先证明了这里с是一正的常数。H.von科赫于1901年在黎曼假设（见黎曼ζ函数）下证明了O(xlnx)。
И.М.维诺格拉多夫等于1958年借助于他的三角和估计方法,得到π(x)-lix=O(xexp(-с(lnx)))，ε为任意正数，с是和ε有关的正常数。误差项π(x)-lix的变化是极不规则的。设ƒ(x)是实函数，如果存在与x无关的正常数α，使得任意大的x满足ƒ(x)>αx，则记为ƒ(x)=Ω(x)；若使得任意大的x满足ƒ(x) <- αx，则记为ƒ(x)=Ω-(x)。若这两种情形同时出现，则记为ƒ(x)=Ω(x)。J.E.李特尔伍德于1914年证明了：当x→∞时，有π(x)-lix=Ω((xlnlnlnx)/lnx)。

算术级数中的质数定理

P.G.L.狄利克雷于1837年首先证明了首项与公差互素的算术级数中有无限多个质数。设整数q≥3.1≤l≤q，(l,q)=1。以π(x,q,l)表首项为l、公差为q的算术级数中不超过x的质数之个数。类似于质数定理，对于固定的q，容易证明： 式中φ(q)表示不超过q且与q互素的正整数的个数。这就是通常所说的算术级数中的质数定理。关于误差项估计，A.佩奇于1935年和C.L.西格尔与A.瓦尔菲施于1936年证明了：对任意正数h，当3≤q≤(lnx)时，有 \[\pi(x,q,l)-{\frac{1}{\phi(q)}}\ln{x}=O(xe^{-c\sqrt{\ln{x}}})\] 式中с为绝对正常数；记号O中所含的常数仅与h有关，而与q无关。

算术级数中的最小质数

设k≥3，1≤l≤k，(l,k)=1。以p(k,l)表算术级数knl(n=0,1,2,…)中的最小质数。S.乔拉猜测p(k,l)=O(k)，其中ε为任意小的正数。ю.Β.林尼克于1944年首先证明了存在绝对常数с，使得p(k,l)=O(k)。潘承洞于1957年首先指出с是可以计算的，并定出了с的值。目前最好的结果с≤17是陈景润于1979年得到的。

相邻质数之差

设pn是第n个质数，是相邻的两个质数之差。在黎曼假设下,H.克拉默于1921年证明了无条件结果是赫斯－布朗和H.伊瓦尼克于1979年得到的。另一方面，关于dn的下界，E.邦别里和H.达文波特于1966年证明了：M.N.赫胥黎于1977年改进为E≤0.4425。猜测应有E=0。关于dn还有许多有趣的研究。

猜想：黎曼ζ函数的所有非平凡零点的实部都等于1/2。

如果用复平面表示黎曼猜想：黎曼ζ函数的所有非平凡零点都在实部等于1/2的临界线上。

黎曼猜想（或称黎曼假设）是关于黎曼ζ函数ζ(s)的零点分布的猜想，由数学家波恩哈德·黎曼于1859年提出。黎曼观察到，质数的频率紧密相关于一个精心构造的所谓黎曼zeta函数ζ(s)的性态。复平面上使黎曼ζ 函数取值为零的点被称为黎曼ζ函数的零点。s=-2n （n 为正整数）是黎曼ζ 函数的零点，这些零点分布有序、 性质简单，被称为黎曼ζ 函数的平凡零点 (trivial zero)。除了这些平凡零点外，黎曼ζ函数还有许多其它零点，它们的性质远比那些平凡零点来得复杂，被称为非平凡零点 (non-trivial zeros)。
在黎曼猜想的研究中， 数学家们把复平面上 Re(s)=1/2 的直线称为 critical line（临界线）。运用这一术语，黎曼猜想也可以表述为：黎曼ζ 函数的所有非平凡零点都位于 critical line 上。即黎曼ζ 函数的所有非平凡零点都位于复平面上 Re(s)=1/2 的直线上（Re(s)表示复数s的实数部分）。

德国数学家戴维·希尔伯特在第二届国际数学家大会上提出了20世纪数学家应当努力解决的23个数学问题，其中便包括黎曼假设。现今克雷数学研究所悬赏的世界七大数学难题中也包括黎曼假设。
当今数学文献中已有超过一千条数学命题以黎曼猜想（或其推广形式）的成立为前提。
黎曼猜想与费马大定理已经成为广义相对论和量子力学融合的m理论几何拓扑载体。
要理解黎曼猜想非常不容易，因为需要复变函数的知识。
目前人们认为它是整个数学界最重要、最著名的那“一个”未解之谜。

猜想：ζ(k)是不是超越数？

超越数是那些不能表示成整系数多项式方程的解的数，它是无理数的一个真子集。
例如 \(\sqrt{2}\) 是无理数，但它不是超越数，因为它是整系数多项式方程 \(x^2-2=0\) 的解。而π已经被证明是超越数，由此得到一个重大结果：经典尺规作图“化圆为方”无解，因为你不可能通过有限次操作得到 \(\sqrt{π}\)。当k为正偶数时，已经证明了ζ(k)必然是超越数。

对于k为正奇数的情形来说，ζ(k)是不是超越数目前还不知道答案。

猜想：R(5,5)等于多少？

有这么一个定理：6个人参加一个聚会，其中某些人之间握过手，那么一定存在3个人互相之间都握过手，或者3个人互相之间都没握过手。我们可以借助鸽笼原理④很快证明这个结论。选出其中一个人A，然后把剩下的5个人分成2组，和A握过手的，以及没和A握过手的。显然，其中一组至少有3个人。不妨假设和A握过手的那一组至少有3个人吧。(在另一种情况下，下述推理同样适用。)把这一组里的3个人分别记作B、C、D(如果这一组的人数大于3，任意选3个人就行了)。如果B、C、D这3个人之间有2个人握过手，那么这2个人和A就成了互相之间握过手的3人组；如果B、C、D这3个人之间都没握过手，那么他们本身就成了互相之间都没握过手的3人组。

④假设有”只鸽子飞回m个笼子，如果n>m的话，那么一定有至少一个笼子，它里面有不止一只鸽子。事实上，至少有一个笼子，它里面有不少于 \(\left\lceil{\frac{n}{m}}\right\rceil\) 只鸽子，其中 \(\left\lceil{x}\right\rceil\) 表示大于等于x的最小整数。鸽笼原理是组合数学中的一个重要工具，今后我们还会用到。

1930年，英国数学家弗兰克·拉姆齐(Frank Ramsey)证明了一个更强的结论：给定两个正整数r和S，总能找到一个n，使得一场n人聚会中，或者存在r个人互相之间都握过手，或者存在s个人互相之间都没握过手。我们把满足条件的最小的n记作R(r，s)。
前面我们已经证明了，6个人足以产生互相都握过手的3个人或者互相都没握过手的3个人，也就是说R(3，3)≤6。但5个人是不够的，比方说只有A和B、B和C、C和D、D和E、E和A之间握手，容易看出不管选哪3个人，握过手的和没握过手的总是并存的。因此，R(3，3)精确地等于6。
求出R(r，s)的精确值出人意料地难。目前已经知道R(4，4)=18，但对于R(5，5)，我们只知道它介于43到49之间，具体的值至今仍未求出来。如果要用计算机硬求R(5，5)，则计算机需要考虑的情况数大约在 \(10^{300}\) 这个数量级，这是一个不可能完成的任务。而R(6,6)更大了，目前已知它在102到165的范围内。它的准确值是多少，恐怕我们永远都不可能知道了。

拉姆赛定理是图论中的组合数学定理，描述当人数达到一定数量时必然出现特定结构的规律。其基本形式指出：在任意6人聚会中，至少有3人互相全部认识或全部不认识，对应的拉姆赛数记为r(3，3)=6。人数不足6时该结论不成立。
该定理采用图论模型，用节点表示人，红蓝边分别表示认识与不认识关系。对于6个节点的完全图进行任意红蓝边着色后，必存在同色三角形。定理可推广为寻找确保k人全连接或l人全不连接的最小人数N，记为r(k，l)。但确定更大的拉姆赛数极为困难，例如已知r(4，4)=18，更大数值尚未明确。
定理由英国数学家弗兰克·拉姆赛于1930年提出并证明其存在性，成为拉姆赛理论的奠基性成果。其核心结论表明对于任意自然数k与l，对应的拉姆赛数r(k，l)必然存在且唯一，但具体计算仍属组合数学未解难题。
什么叫拉姆塞数？拉姆塞理论概念是：给定足够多的样本，那么任何复杂的结构都会必然出现。例如有一个著名的定理：6个人中必然有3个人互相认识或者3个人互相不认识。换一种说法，6个点之间两两连线，每条线都是红色或蓝色，那么必然会出现一个红色三角形或者一个蓝色三角形。这个定理用拉姆塞理论的语言说，就是R(3，3)=6。给定两个自然数s和t，拉姆塞数R(s，t)的意思是：达到这么多人，其中就必然有s个人互相认识或者t个人互相不认识。拉姆塞证明了，这样的数必然存在。然而确定拉姆塞数的难度上升得极快。目前已经知道R(1，1)=1，R(2，2)=2，R(3，3)=6，R(4，4)=18，但再往上我们就不知道了。对于R(5，5)，可以确定它在43到48之间，但具体是多少仍然不知道。对于更大的n更是一头雾水。

猜想：除了n=4的情况外，是否不存在n阶循环Hadamard矩阵？

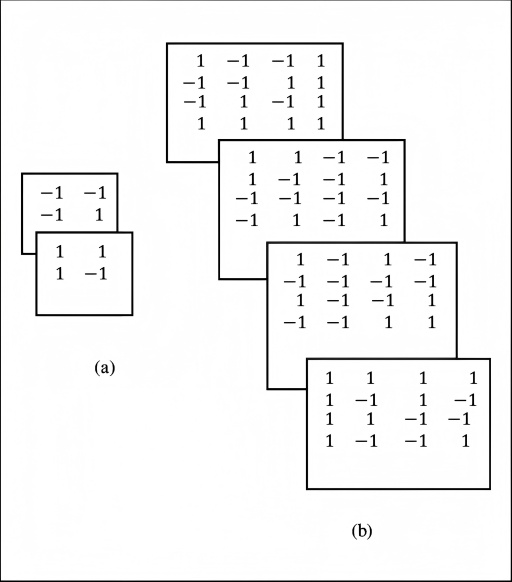
循环Hadamard矩阵是一种特殊的矩阵，它同时满足Hadamard矩阵和循环矩阵的性质。具体定义如下：
·Hadamard矩阵性质：一个n阶方阵H，其元素取值为+1或-1，并且满足，其中 \(H^T\) 是H的转置矩阵，I是n阶单位矩阵。
·循环矩阵性质：矩阵H的每一行都是由前一行的元素循环右移一个位置得到的。等价地说，对于 \(H^T\) ，H的第2+1行是第i行向右循环移动一位得到的，而H的第一行是第n行向右循环移动一位得到的。
同时满足上述两个条件的矩阵H就被称为n阶循环Hadamard矩阵。

循环Hadamard猜想是组合数学中与Hadamard矩阵相关的一个重要猜想。
这一猜想是 Ryser 有关循环差集猜想的一个推论，故可认为循环 Hadamard 猜想起源于 Ryser。循环 Hadamard 矩阵是一种特殊的 Hadamard 矩阵，它既是 Hadamard 矩阵，又是循环矩阵。循环矩阵是指其每行元素都是由前一行元素循环右移得到的矩阵。

目前该猜想的研究已取得一定成果。例如，Leung和Schmidt利用深刻的代数和数论工具证明了如果n不满足某些条件，则不存在n阶循环Hadamard矩阵。2011年，Barry Hurley和Paul Hurley证明了对于 \(4n\times4n\) 的循环Hadamard矩阵，n=1，即除了4阶循环Hadamard矩阵外，不存在其他阶数的循环Hadamard矩阵，这在很大程度上支持了循环Hadamard猜想。

猜想：\(C_{1/2}={\frac{2}{1+\sqrt2}\approx0.828427}\)

如果从数字序列A中删除一些数字就能得到数字序列B，我们就说B是A的子序列。例如，110是010010的子序列，但不是001011的子序列。两个序列的“公共子序列”有很多，其中最长的那个就叫做“最长公共子序列”。

随机产生两个长度为n的01序列，其中数字1出现的概率是P,数字0出现的概率是1-p。用\(C_p(n)\)来表示它们的最长公共子序列的长度，用 \(C_p\), 来表示当n无穷大时 \(\frac{C_p(n)}{n}\) 的极限值。
关于 \(C_p\) 的存在性，有一个非常巧妙的证明；然而，这个证明仅仅说明了 \(C_p\) 存在，它没有给计算 \(C_p\) 带来任何有用的提示。
即使是 \(C_{1/2}\) 的值，也没人能成功算出来。迈克尔·斯蒂尔(Michael Steele)猜想 \(C_{1/2}={\frac{2}{1+\sqrt2}\approx0.828427}\) 。后来，瓦克拉夫·克沃特尔(Vaclav Chvátal)和戴维·桑科夫(David Sankoff)证明了 \(0.773911{\lt}{C_{1/2}}{\lt}0.837623\) ,看上去迈克尔·斯蒂尔的猜想似乎很可能是对的。
2003年，乔治·利克(George Lueker)证明了 \(0.7880{\lt}C_{1/2}{\lt}0.8263\),推翻了迈克尔·斯蒂尔的猜想。
更糟的是，“当p=2时CD达到最小”似乎是一件很靠谱的事，但这个结论也无人能证明。

猜想：克拉科斯基数列的第n项有非递归的公式吗？

Kolakoski序列是仅由1和2组成的无限自描述数列，OEIS编号A000002。其通过递归分组规则生成：首项为1，第二项为2，后续项的值与前序分组的长度相等，形成非循环结构。
该数列具有独特的分形特性：对其游程编码（合并相邻重复项）所得结果仍为原序列。例如前三项确定后，后续项由前序分组长度依次生成。这一机制使序列在扩展过程中展现出内在递归性。
自提出以来，Kolakoski序列的数学性质引发诸多猜想与研究。Chvátal证明了1的密度上限为0.50084，但1和2的极限比例是否趋近于1/2尚未被证实。目前尚未发现通项公式，其生成机制与数论属性的关联仍是组合数学领域的研究焦点。

克拉科斯基(Kolakoski)数列是一个仅由1和2构成的数列，其中头100个数是：
1，2，2，1，1，2，1，2，2，1，2，2，1，1，2，1，1，2，2，1，2，1，1，2，1，2，2，1，1，2，1，1，2，
1，2，2，1，2，2，1，1，2，1，2，2，1，2，1，1，2，1，1，2，2，1，2，2，1，1，2，1，2，2，1，2，2，
1，1，2，1，1，2，1，2，2，1，2，1，1，2，2，1，2，2，1，1，2，1，2，2，1，2，2，1，1，2，1，1，2，2，...

如果我们把连续的相同数看做一组的话，整个数列的定义就只有两句话：a(1)=1，a(n)表示第n组数的长度。
注意，有了这几个条件，整个序列就已经唯一地确定了!a(1)=1就表明第一组数只有一个数(也就是它自己)，因此下一个数必须要换成2，也就是a(2)=2；而a(2)=2又说明第二组数(也就是a(2)所在的这组数)有两个数，因此a(3)也等于2；而a(3)=2就表明第三组数的长度为2，即数列接下来要有两个1，等等。也就是说，这个数列完全是“自生成”的。更酷的说法则是，如果把每一组数用它的长度来替换，得到的仍然是这个数列本身。
关于克拉科斯基数列，我们知道些什么?很少。贝诺瓦·克罗伊特(Benoit Cloitre)发现，这个数列可以用递归式 \(a(a(1)+a(2)+...+a(k))={\frac{3+(-l)^k}{2}}\) 来表达。德金(F.M.Dekking)证明了一个看上去更妙的结论：去掉数列最前面的1，剩下的部分可以从22开始，每次按22→2211，21→221，12→211，11→21的规则两位两位地对数列进行替换，并不断迭代产生。不过，这些发现都不足以让我们更加深入地了解克拉科斯基数列。
克拉科斯基数列的第n项有非递归的公式吗?目前我们还不知道。已经出现过的数字串今后都还会再次出现吗?目前我们也不知道。还有，我们有理由猜想，数列中1和2的个数各占一半。图1显示的就是数列前”项中数字1所占的比例，可见我们的猜想很可能是对的。
不过，目前还没有人能够证明这一点。而最近的一些研究表明，数字的比例很可能开果。当然，还有第三种可能——这个极限可能根本不存在。

猜想：对于每一个人，总会有一个时刻，他与其他所有人的距离都不小于1/n。

有一个环形跑道，总长为1个单位。n个人从跑道上的同一位置出发，沿着跑道顺时针一直跑下去。每个人的速度都是固定的，但不同人的速度不同。证明或推翻，对于每一个人，总会有一个时刻，他与其他所有人的距离都不小于1/n。这个问题是由威尔斯(J.M.Wills)在1967年提出的。乍看上去，这个问题无异于其他各种非常巧妙的初等组合数学问题，但不可思议的是，这个问题竟然直到现在仍没彻底解决。

当n=2时，由于两人的速度不同，因此到了某个时刻，他们必然会位于环形跑道的两个对称位置上，他们到对方的距离都恰好等于1/2。可见n2时命是异成立的此后，数学家们后证明了n=3、n=4、n=5和n=6的情形。直觉上，对于更大的n，结论也应该成立，不过尚未有人证明。

猜想：是否存在线条数大于顶点数的Thrackle？

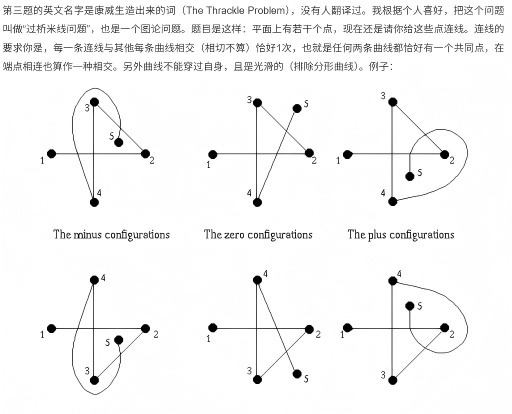
题目是这样：平面上有若干个点，现在还是请你给这些点连线。连线的要求你是，每一条连线与其他每条曲线相交（相切不算）恰好1次，也就是任何两条曲线都恰好有一个共同点，在端点相连也算作一种相交。另外曲线不能穿过自身，且是光滑的（排除分形曲线）。
在纸上画一些点，再画一些点与点之间的连线，我们就把所得的图形叫做一个“图”。如果一个图的每根线条都与其他所有线条恰好相交一次(顶点处相接也算相交),那么就把这个图叫做一个thrackle。图6显示的就是三个满足要求的thrackle,注意到它们的线条数量都没有超过顶点的数量。问，是否存在线条数大于顶点数的thrackle?


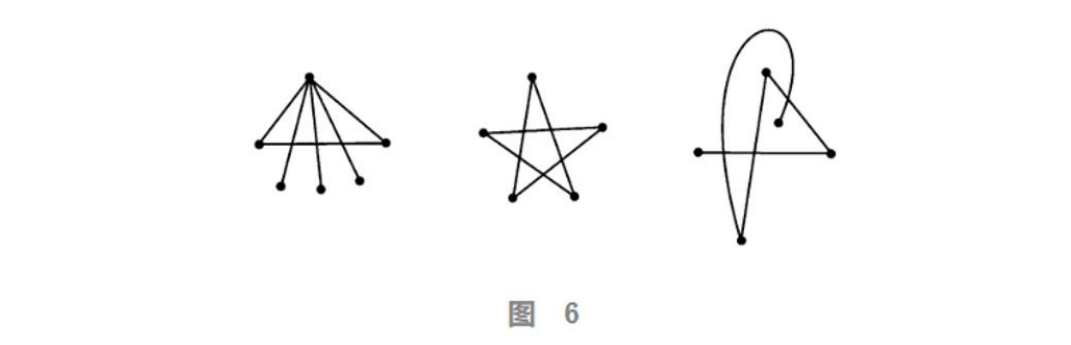
这个问题是由数学家约翰·康威提出来的。这明显又是一个坑，看到这个问题谁都想试试，然后就纷纷崩溃掉。康威悬赏1000美元征解，可见这个问题有多么不容易。目前已知的最好的结果167是，一个thrackle的线条数不会超过顶点数的 167/117 倍。

猜想：在n维空间中，最多可以有多少个曼哈顿距离两两相等的点？

很多城市的交通系统都是由大量横纵街道交错构成的，纽约的曼哈顿区就是最为典型的例子。因此，在估算两地之间的距离时，我们往往不会直接去测量两地之间的直线距离，而会去考虑它们在横纵方向上一共相距多少个街区。在数学中，我们就把平面上两个点的横坐标之差与纵坐标之差的和叫做这两点之间的曼哈顿距离。例如，(0，0)和(3，4)两点间的直线距离是5，但曼哈顿距离则是7。

这个定义可以很自然地推广到n维空间中去。定义n维空间中 \(P(p_1,p_2,...,p_n\) 和 \(Q(q_1,q_2,...,q_n\) 两点之间的曼哈顿距离为\(|p_1-q_1|+|p_2-q_2|+...|p_n-q_n|\) ，直观地说，就是在n维网格中从P到Q的最短路径长度。一个与此相关的数学未解之谜：在n维空间中，最多可以有多少个曼哈顿距离两两相等的点?

容易看出，这样的点至少可以有2n个，例如三维空间中(1，0，0) (-1，0，0)、(0，1，0)、(0，-1，0)(0，0，1)、(0，0，-1)就是满足要求的6个点。大家肯定会想，这应该就是点数最多的方案了吧?不过，真要证明起来可没那么容易。1983年，罗伯特·库斯纳(Robert Kusner)猜想，n维空间中曼哈顿距离两两相等的点最多也只能有2n个，这也就是现在所说的库斯纳猜想。目前人们已经证明，当n≤4时，库斯纳猜想是正确的。当n>4时呢?虽然大家相信这个猜想也应该是正确的，但还没有人能够证明。

有趣的是，在很多其他的度量空间下，同类型的问题却并没有这么棘手。如果把距离定义为标准的直线距离，那么n维空间中显然最多有n+1个等距点；如果把距离定义为切比雪夫(Chebyshev)距离(即所有 \(|p_i-q_i|\) 中的最大值)，问题的解则是 \(2^2\)，即n维坐标系中单位立方体的 \(2^2\) 个顶点。一旦换作曼哈顿距离，问题就迟迟不能解决，这还真有些出人意料。

猜想：证明或推翻，你可以通过每次添加或者删除一个元素，循环遍历集合{1，2，…，2n+1}的所有大小为n或n+1的子集。

例如，当n=2时，你可以通过以下路径循环遍历{1，2，3，4，5}的所有包含2个元素或者3个元素的子集：
{1，2}→{1，2，3}→{1，3}→{1，3，4}→{1，4}→{1，2，4}→{2，4}→
{2，4，5}→{4，5}→{1，4，5}→{1，5}→{1，3，5}→{3，5}→{3，4，5}→
{3，4}→{2，3，4}→{2，3}→{2，3，5}→{2，5}→{1，2，5}→{1，2}

看完上面的这段内容，我可以想象你已经有一种克制不住的冲动，拿起铅笔和草稿纸，或者跑到电脑前，开始寻找n不大时的规律。这可以说是本文的所有问题中最大的一个坑了——这个问题极具诱惑性，任何人第一次看到这个问题时都会认为存在一种对所有n都适用的构造解，于是众人一个接一个地往坑里跳，拦都拦不住。

几乎没有人认为这个猜想是错误的。目前计算机已经验证了，当n≤17时，猜想都是成立的。从已有数据来看，随着n的增加，遍历这些子集的方案数不但也随之增加，而且增长得非常快。到了某个n，方案数突然跌到了0，这明显是一件极不可能发生的事。但是，几十年过去了，却没有人能够证明它!

猜想：一定能找到某个元素，它在至少一半的集合里出现。

令U是一个有限集合，\(S_1,S_2,...,S_n\) 都是U的非空子集，它们满足任意多个集合的并集仍然在这些集合里。证明，一定能找到某个元素，它在至少一半的集合里出现。
不可思议，即使是最基本最离散的数学研究对象——有限集合——里面，也有让人崩溃的未解问题。
1999年，彼达斯·沃伊奇克(Piotr Wojcik)用一种非常巧妙的方法证明了，存在一个元素在至少 \(\frac{n}{\log_{2}n}\) 个集合里出现。不过，这离目标还有很大一段距离。

猜想：在n维欧几里得空间中，任何直径为1的集合都可以被分割成n + 1个直径小于1的子集。例如，在二维平面中，任何直径为1的图形都可以被分成3个直径小于1的部分；在三维空间中，任何直径为1的物体都可以被分成4个直径小于1的部分。

博舒克猜想是离散几何中的一个著名问题，由波兰数学家卡罗尔・博舒克（Karol Borsuk）于 1932 年提出。

研究进展
部分证明：该猜想在n = 2（平面情况）和n = 3 （三维空间情况）以及一些特殊情形下已被证明是正确的。比如，对于n = 2，可以通过一些几何构造和推理来证明任何直径为1的平面图形都能按要求分割。
反例出现：
1993 年，杰夫・卡恩（Jeff Kahn）和吉尔・卡拉伊（Gil Kalai）找到了一个反例，表明在n = 1326及更高维度时，博舒克猜想不成立。他们的研究表明，在高维空间中，存在一些集合无法按照博舒克猜想的方式进行分割。2003 年，欣里希斯（Hinrichs）和里希特（Richter）进一步构造出了\(n\geq298\)时的有限集反例。
2013 年，安德烈・V・邦达连科（Andriy V. Bondarenko）证明了对于所有n大于等于65，博舒克猜想是错误的。不久之后，托马斯・延里希（Thomas Jenrich）从邦达连科的构造中得到了一个64维的反例，这是目前已知的最低维反例。

尽管博舒克猜想在一般情况下已被证明不成立，但它仍然是离散几何领域中一个重要的研究课题，激发了许多相关的研究和探索，推动了离散几何、组合数学等领域的发展。数学家们仍在继续研究与博舒克猜想相关的问题，例如寻找在哪些特殊条件下该猜想仍然成立，以及研究相关的几何性质和组合结构等。

猜想：给定一个整体域上的阿贝尔簇(通常考虑椭圆曲线),猜想其莫代尔群的秩等于它的L函数在1处的零点阶数，且它的L函数在1处的泰勒展开的首项系数与莫代尔群的有限部分大小、自由部分体积、所有素位的周期以及沙群有精确的等式关系。前半部分通常称为弱BSD猜想。简单来说，就是通过椭圆曲线的L函数在s=1处的性质来刻画椭圆曲线有理点群的结构。

贝赫和斯维讷通 - 戴尔猜想（Birch and Swinnerton - Dyer 猜想），简称 BSD 猜想，是世界七大数学难题之一，属于数论领域中椭圆曲线相关的重要未解难题。猜想背景：该猜想由英国数学家布莱恩·约翰·贝赫(Bryan John Birch)和彼得·斯维讷通-戴尔(PeterSwinnerton-Dyer)在20世纪60年代提出。其与椭圆曲线紧密相关，椭圆曲线是形如\(y^2=x^3+ax+b\) (a、b为有理数)的函数曲线，其有理数解构成一个阿贝尔群。莫代尔定理表明，整体域上的阿贝尔簇(椭圆曲线是一种特殊的阿贝尔簇)的有理点形成一个有限生成交换群，这为BSD猜想的提出奠定了基础。

已知结果：对于解析秩为0的情形，科茨(Coates)、怀尔斯(Wiles)、科利瓦金(Kolyvagin)、鲁宾(Rubin)、斯金纳(Skinner)、厄本(Urban)等人证明了弱BSD猜想，并且精确的BSD猜想在2以外均成立；对于解析秩为1的情形，格罗斯(Gross)、扎吉尔(Zagier)等人证明了弱BSD猜想，并且精确的BSD猜想在2和导子以外均成立。

猜想的推论：由BSD猜想可以推出奇偶性猜想、西尔维斯特等很多猜想。其中最著名的是与同余数问题的关系，从BSD猜想可以推出模8余5、6、7的无平方因子的正整数一定可以成为某个有理边长直角三角形的面积。

由于其重要性和难度，BSD 猜想被克雷数学研究所列为七个千禧年大奖难题之一，若有人能给出正确证明，将获得该研究所提供的700万美元奖金。

射影平面是射影几何中的一个基本概念，它是在欧氏平面的基础上通过添加一些 “无穷远点” 和 “无穷远直线” 而得到的一种几何结构。
以下是关于射影平面的详细介绍：
定义与构造
在欧氏平面中，任意两条平行直线在无穷远处似乎会相交于一个 “无穷远点”。为了使任意两条直线都有交点，我们给每一组平行直线添加一个无穷远点。所有这些无穷远点构成了一条 “无穷远直线”，将其与欧氏平面原有的点和直线一起，就构成了射影平面。
主要性质
点线关联性质：在射影平面中，任意两个不同的点确定唯一一条直线，任意两条不同的直线相交于唯一一点。这一性质消除了欧氏平面中平行直线无交点的特殊情况，使得点和直线的关系更加对称和统一。
对偶原理：射影平面具有对偶性，即对于射影平面中的一个关于点和直线的命题，如果将其中 “点” 与 “直线” 的概念互换，同时将 “点在直线上” 与 “直线通过点” 等相关表述也进行互换，所得到的新命题依然成立。例如，“两点确定一条直线” 的对偶命题是 “两直线确定一个点”。
表示方法
齐次坐标表示：射影平面中的点通常用齐次坐标来表示。
对于平面上的一个点(x,y),在射影平面中其齐次坐标可以表示为(x1,x2,x3),其中\(x=\frac{x1}{x3}\),\(y=\frac{y1}{y3}\)(x3≠0)。当x3=0时，表示的是无穷远点。通过齐次坐标，可以方便地进行射影变换等操作，并研究射影平面上的几何性质。
射影平面在数学的多个领域，如代数几何、组合数学以及计算机图形学等中都有重要的应用。它为解决一些在欧氏几何中较为复杂的问题提供了新的思路和方法。